Partie I : le filtrage
I. Introduction et définitions
Problématique : Quand l’on utilise un signal représentant des données, qu’il soit à l’origine analogique et numérique, son transport (par fils, par ondes, ….) se fait de manière analogique et souvent avec la technologie électrique (ou lumineuse). Il apparaît alors des parasites.
Exemple : signal numérique :
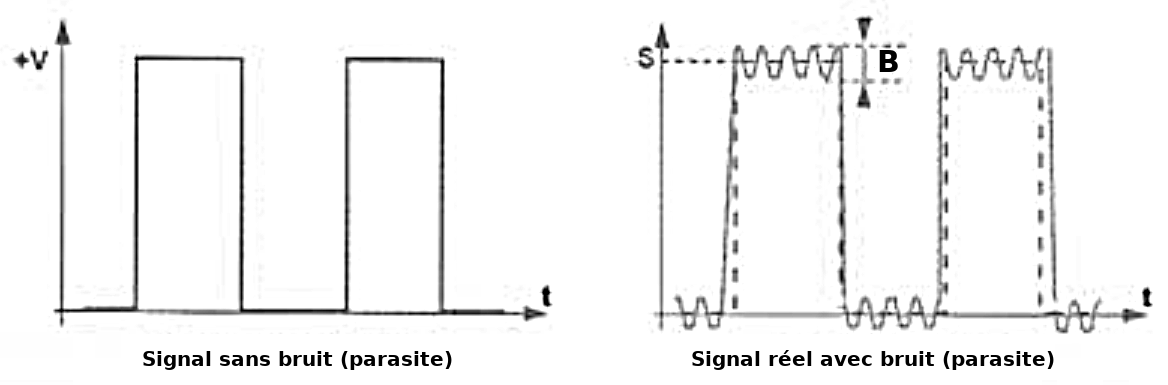
Si le bruit B devient trop important en amplitude on voit bien qu’il risque de modifier le sens du signal en créant des 0 ou des 1 non voulus. On le voit bien sur l’exemple précédant, la fréquence du bruit est très différente de celle du signal. Le filtrage va nous permettre d’éliminer la partie non voulue du signal.
Principe :
Le filtrage (analogique) est obtenu en envoyant le signal à travers un ou plusieurs circuits électroniques, qui modifient le signal afin de le rendre conforme à ce que l'on souhaite (en terme de forme, de fréquence, d'amplitude, ....)
Souvent le but du filtrage est d’éliminer (ou plutôt de diminuer) les parasites indésirables. Mais il peu aussi avoir pour rôle d’isoler la partie utile de notre signal (qui fait alors parti d'un signal plus complexe).
Fonction de transfert
Une fonction de transfert est une représentation mathématique de la relation entre l'entrée et la sortie d'un système linéaire.
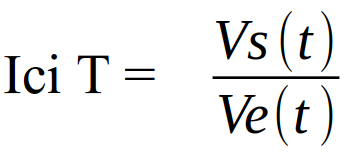
Remarque : on travaille souvent avec les nombres complexes (voir cours de mathématique). La fonction de transfert T sera alors caractérisée par un module (gain) et un argument.
Le résultat sera alors noté :
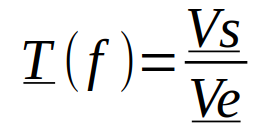
Gain d'un filtre
Le gain désigne la capacité d'une fonction (ici la fonction « FILTRE ») à augmenter ou diminuer la valeur du signal d’entrée (Ve). Le gain est soit un chiffre sans dimension soit il est exprimé en dB (décibels) notamment quand on travaille sur le filtrage.
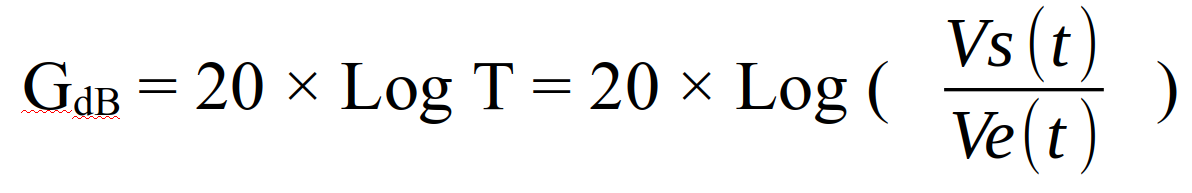
Log est la fonction mathématique Logarithme
Rappel mathématique: si vous voulez faire le calcul inverse de GdB=20×Log G, c’est à dire retrouver G, il faut faire la fonction inverse de log. Ainsi G = 10(GdB/20).
Passif ou actif ?
Un filtre passif fait appel à des éléments passifs (résistances, condensateurs ou bobines). En conséquence le signal de sortie ne peut jamais être supérieur au signal d'entrée.
Un filtre actif est composé d'éléments actifs (transistors, amplificateurs opérationnels...) qui permettent d'avoir des amplitudes du signal de sortie supérieures aux amplitudes du signal d'entrée.
Échelle semi-logarithmique
Nous allons utiliser une échelle dite « semi-logarithmique ». Il s’agit d’un repère dans lequel l'un des axes, pour nous celui des abscisses (x), est gradué selon une échelle logarithmique (log) et celui des ordonnées (y) est gradué selon une échelle linéaire (la forme « classique »). Cette échelle permet d’avoir de grandes valeurs sur les axes.
Cela donne :
On remarque que l’écart entre 1 et 10 est le même qu’entre 10 et 100 et qu’entre 100 et 1000 !
Explications :
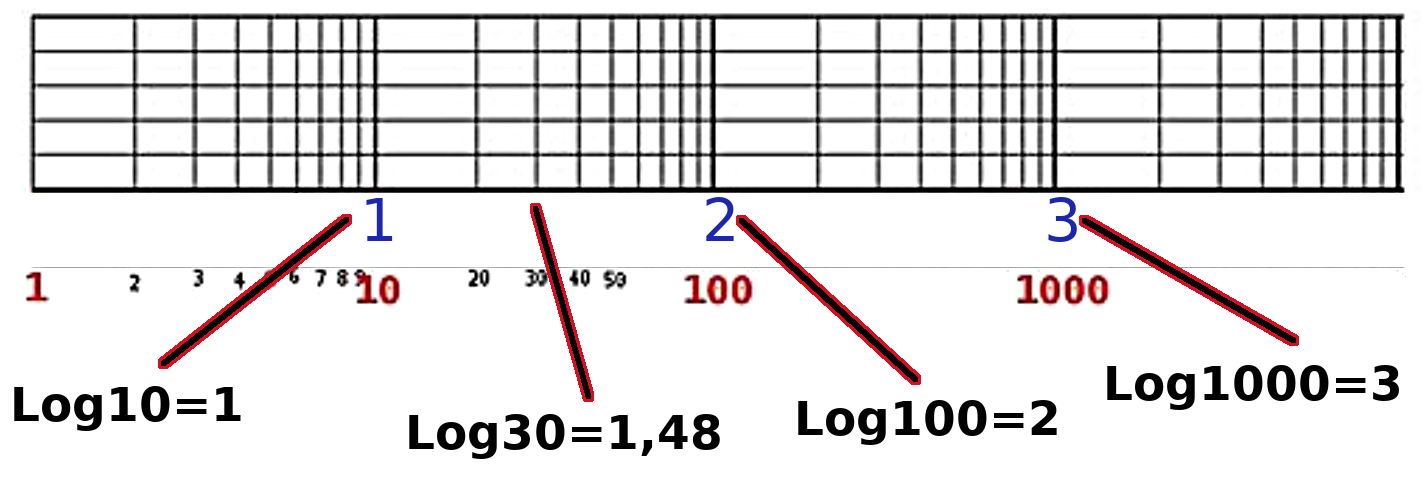
Ainsi entre 2 valeurs de la partie logarithmique, les valeurs sont multipliées par 10.
Si on compare les 2 types d’échelle :
Diagramme de Bode :
Le diagramme de Bode est un moyen de représenter le comportement fréquentiel d'un système. Il permet une résolution graphique simplifiée, en particulier pour l'étude des fonctions de transfert de systèmes analogiques et donc notamment du filtrage.
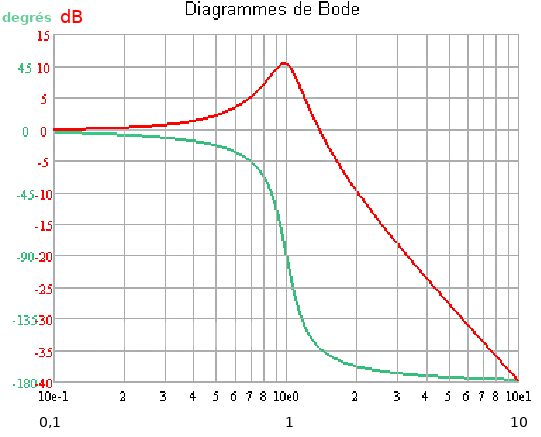Le diagramme de Bode est constitué de deux graphiques :
- Le premier graphique est la représentation du gain exprimé en décibel(dB) en fonction de la pulsation (ω, rad/s), de la fréquence (F, Hz) ou du rapport F/Fc (Fc = Fréquence de coupure) voir du rapport ω/ωc.
- Le second graphique est la représentation de la phase (argument) exprimé en radians ou en degrés toujours en fonction de la pulsation (ω, rad/s), de la fréquence (F, Hz) ou du rapport F/Fc (Fc = Fréquence de coupure).
Exemple ici à droite: en rouge le gain, en vert la phase
Ordre d'un filtre
L'ordre d'un filtre définit sa capacité à atténuer les fréquences. Plus l'ordre est élevé, plus la pente de l’intervalle de fréquence (on travaille soit en décade soit en octave) et de l'amplification est élevée.
Ainsi un filtre du :
- 1° ordre atténue les fréquences de 20 dB par décade (ou 6 dB/octave)
- 2° ordre atténue les fréquences de 40 dB/décade
Remarques :
- 1 décade correspond à un écart de fréquence de 10 (F2 = 10 × F1 par exemple)
- 1 octave correspond à un écart de fréquence de 2 (F2 = 2 × F1 par exemple)