Erreurs absolue - relative

Erreur absolue


L'erreur absolue mesure l'imprécision sur une mesure que nous effectuons.

L'erreur absolue est : δα = valeur approchée - valeur réelle


Elle est appelée absolue, car elle est le résultat de la valeur absolue de la différence entre d'une part la valeur réelle de la grandeur que l'on mesure et d'autre part une valeur de référence que nous avons choisie comme une bonne approximation de celle-ci.

Elle est donc toujours un nombre positif.

Si on note x la valeur réelle, α la valeur de référence, et δα l'erreur absolue, on peut écrire :

            δα = |α-x| = |x-α|


Par exemple, si nous souhaitons mesurer une longueur en centimètres et que cette longueur est supérieure ou inférieure de moins de 0,5cm à une valeur de référence α en centimètres, on a :

δα < 0,5

Ce qui se traduit par un intervalle de valeurs pour x (valeur réelle de la longueur) :
   |α-x| < 0,5
   Soit : α-0,5 < x < α+0,5
   Ou encore : x est dans l'intervalle [ α-0,5 ; α+0,5 ]

  
Erreur relative

L'erreur relative est :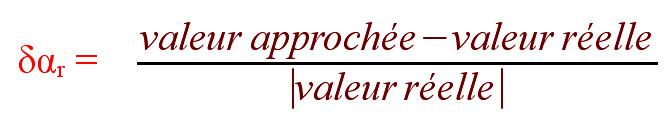
ou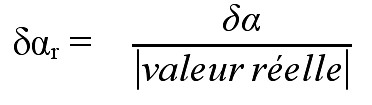

     
remarque : l'erreur relative est souvent exprimée en %



Le résultat donne un rapport, par exemple 0,14. Cela signifierait que l'erreur relative est de +0,14, soit 14 %.

Remarquons que dans cette définition, il n'y a pas de valeur absolue au numérateur, de sorte qu'il s'agit d'une erreur relative algébrique : si elle est positive, c'est que la valeur approchée est supérieure à la valeur exacte (on parle d'erreur par excès), et si elle est négative, c'est qu'elle est inférieure (erreur par défaut).

Donc la valeur approchée est obtenue par :  (valeur réelle) × (1 + δαr )