I. Fonctions logiques
Les fonctions logiques sont les composants de base de l’électronique numérique. Il en existe de simples comme les fonctions ET (AND en anglais) et de plus complexes.
Il existe une normalisation du nom de ces fonctions logiques, notamment en fonction de leur rôle mathématique (ou logique) et de leur technologie.
Un document ressource est disponible : « Logique et binaire eleves.pdf »
Remarques sur les vidéos: les vidéo utiles sont, en général, intégrées aux pages du site internet dans un format compatible (ne pas hésiter à réactualiser la page en cas de problème). Mais quelques fois cela ne fonctionne pas (les navigateurs seraient-ils capricieux?). Pour cela un autre format de la vidéo est fourni en lien, en général au dessus. Il faut télécharger cette vidéo (clic droit sur le lien, ...) puis la lire avec un logiciel adapté (VLC par exemple)
1. Fonction ET (à 2 entrées)
a) Dessinez les deux logigrammes (norme américaine et norme européenne)
b) On va étudier la simulation la fonction ET à l’aide de la porte correspondante (AND dans le logiciel), de 2 interrupteurs (switch) et d’une lampe placée sur la sortie de la porte.
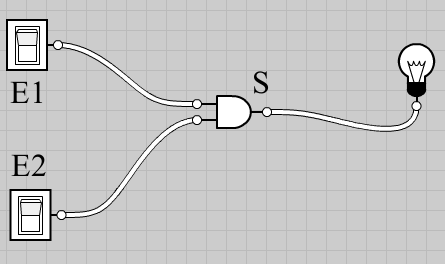
Regardez la vidéo de la simulation: (le lien en cas de problème: video_porte_et.mp4)
|
c) En déduire la table de vérité :
|
Explications de la table de vérité :
E1 et E2 représentent les deux entrées de la porte logique. elles ont donc 2 états possibles : marche (1 logique) et arrêt (0 logique)
S représente la sortie de la porte logique correspondant à l’état de la lampe dans la simulation
Lampe éteinte = 0 logique |
 |
Remarque : l’équation de ce montage est : S = E1 . E2 (le point représente la fonction ET et on lit : S égale E1 et E2) |
On peut faire l’analogie électrique suivante:
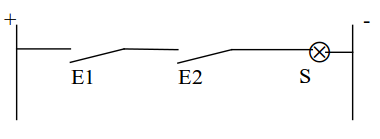
d) Expliquer cette analogie électrique (1 contact = une entrée logique, sortie=lampe). Est-elle correcte ?
2. Fonction OU (à 2 entrées)
a) Dessinez les deux logigrammes (norme américaine et norme européenne)
b) Simulation de la fonction OU et en déduire la table de vérité :
vidéo de l'animation (en cas de problème le lien: video_porte_ou.mp4)
|
E1 |
E2 |
S |
|
0 |
0 |
|
|
0 |
1 |
|
|
1 |
0 |
|
|
1 |
1 |
c) En déduire l’analogie électrique
d) Donner l’équation logique de ce logigramme : S = ........
3. Fonction PAS (NON)
a) Dessinez les deux logigrammes (norme américaine et norme européenne)
b) regardez la vidéo de la simulation de la fonction PAS et en déduire la table de vérité :
vidéo de l'animation (en cas de problème le lien: video_porte_pas.mp4
|
E1 |
S |
|
0 |
|
|
1 |
c) En déduire l’analogie électrique
d) Donner l’équation logique de ce logigramme : S = .............
4. Fonction NOR ou Not Or (à 2 entrées)
a) Dessinez les deux logigrammes (norme américaine et norme européenne)
b) Regardez la vidéo de la simulation de la fonction NOR et en déduire la table de vérité :
vidéo de l'animation (en cas de problème le lien: video_porte_nor.mp4
|
E1 |
E2 |
S |
|
0 |
0 |
|
|
0 |
1 |
|
|
1 |
0 |
|
|
1 |
1 |
c) Donner l’équation logique de ce logigramme : S = .........
5. Fonction NAND ou Not And (à 2 entrées)
a) Dessinez les deux logigrammes (norme américaine et norme européenne)
b) Regardez la vidéo de la simulation de la fonction NAND et en déduire la table de vérité :
vidéo de l'animation (en cas de problème le lien: video_porte_nand.mp4
|
E1 |
E2 |
S |
|
0 |
0 |
|
|
0 |
1 |
|
|
1 |
0 |
|
|
1 |
1 |
c) Donner l’équation logique de ce logigramme : S = ......
6. Fonction XOR (OU exclusif à 2 entrées)
a) Dessinez les deux logigrammes (norme américaine et norme européenne)
b) Regardez la vidéo de la simulation de la fonction XOR et en déduire la table de vérité :
vidéo de l'animation (en cas de problème le lien: video_porte_xor.mp4
|
E1 |
E2 |
S |
|
0 |
0 |
|
|
0 |
1 |
|
|
1 |
0 |
|
|
1 |
1 |
c) Donner l’équation logique de ce logigramme : S = ........
7. Exemple de schéma logique simple (logigramme)
Nous disposons de 3 capteurs de présence (CP1, CP2 et CP3) qui surveillent un petit musée. L'alarme sera déclenché si un des 3 capteurs détecte une présence mais seulement si l'alarme est enclenchée (AL). Nous avons donc 4 variables binaires d'entrée (CP1, CP2, CP3 et AL) et une variable binaire de sortie (ALARME). Nous allons réaliser cette gestion de l'alarme avec un petit circuit logique.
1. Compléter la table de vérité de l'alarme:
- étape 1 : compléter le code binaire des entrées (AL, CP1, CP2 et CP3)
- étape 2 : compléter le code binaire de l’alarme en fonction de l’énoncé
|
AL |
CP1 |
CP2 |
CP3 |
ALARME |
0
|
0
|
0
|
0
|
|
0
|
0
|
0
|
1
|
|
0
|
0
|
1
|
0
|
|
0
|
0
|
1
|
1
|
|
0
|
1
|
0
|
0
|
|
0
|
1
|
0
|
1
|
|
0
|
1
|
1
|
0
|
|
0
|
1
|
1
|
1
|
|
1
|
0
|
0
|
0
|
|
2. Ecrire l'équation logique de l'alarme: ALARME = ( ...... + ...................
3. Compléter le logigramme avec les noms des variables:
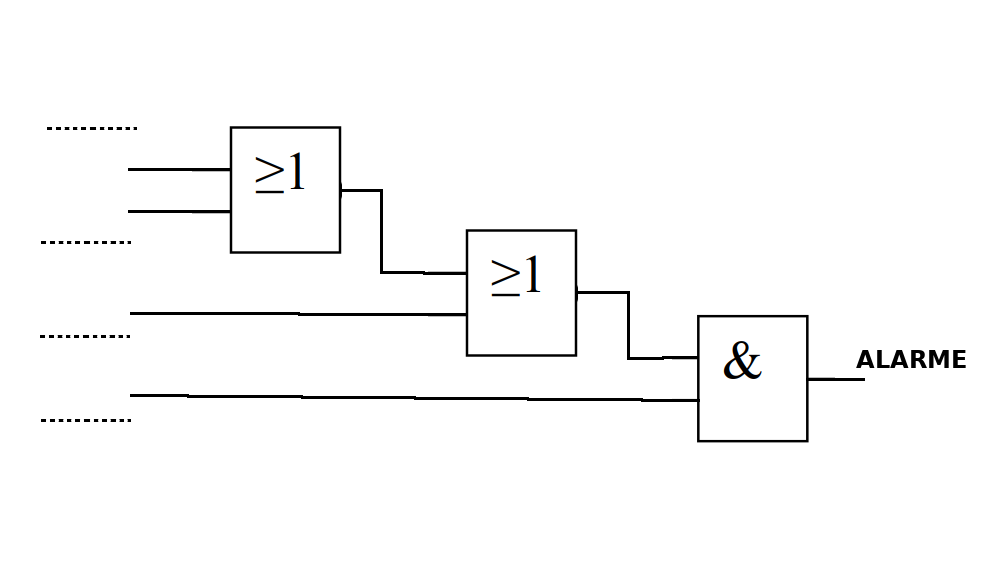
8. Exemple de schéma logique (logigramme)
Soit le logigramme suivant :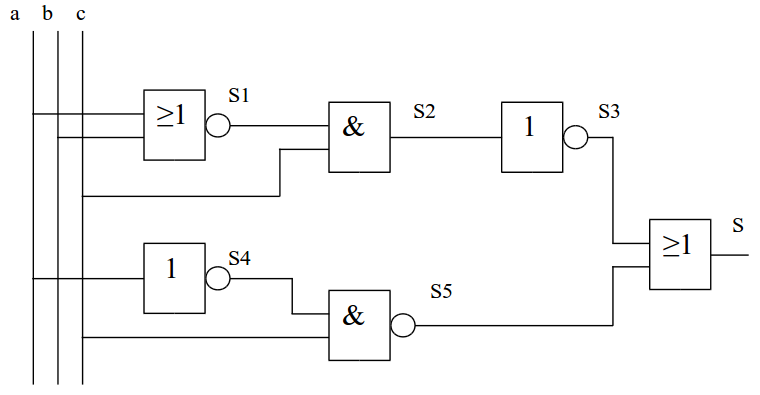
1. Écrire, au dessus de chaque porte logique du logigramme ci-dessus, le nom de la porte logique (ET, OU, …) .
2. Donner l’équation de chaque sortie de portes logiques (S1, S2, S3, S4, S5 et S). Faire valider par le professeur.
S1 =
S2 =
S3 =
S4 =
S5 =
S =
3. Faire, de manière théorique, les tables de vérité de chaque sortie. Faire valider par le professeur.
Remarque: on remplit le tableau, colonne par colonne, à partir des équations déterminées dans la question précédente.
|
a |
b |
c |
S1 |
S2 |
S3 |
S4 |
S5 |
S |
|
0 |
0 |
0 |
||||||
|
0 |
0 |
1 |
||||||
|
0 |
1 |
0 |
||||||
|
0 |
1 |
1 |
||||||
|
1 |
0 |
0 |
||||||
|
1 |
0 |
1 |
||||||
|
1 |
1 |
0 |
||||||
|
1 |
1 |
1 |
Remarque: vous pouvez vérifier votre table de vérité en simulant le montage sur le site: https://logic.ly/demo/