I. Rappels des lois et propriétés des circuits électriques

1.1. Les résistors (abusivement appelés « résistances »)

Symbole officiel :
ou quelques fois:

Effet résistif
On considère un conducteur, aux bornes duquel on impose une différence de potentiel (une tension). Ce conducteur serait alors traversé par un courant électrique. Cependant, tous les matériaux ne "conduisent" pas l'électricité aussi facilement : certains offrent plus ou moins de résistance au passage des électrons. C'est ce phénomène que l'on appelle l'effet résistif.

L’unité de résistance électrique est l’Ohm : Ω

à certaines températures (souvent très basses), il existe des matériaux sans résistance électrique. On les appelle des matériaux supraconducteurs.

Association de résistors

Considérons deux résistances R1 et R2. On peut les associer de deux manières : soit elles sont parcourues par le même courant (association en série), soit elles sont soumises à la même tension (association en parallèle).


1.1.1 Association en série

En série, la résistance équivalente, est la somme des résistances.

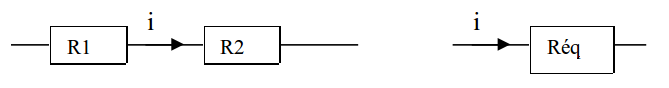
La résistance équivalente est Réq = R1 + R2

Généralisation:

 

1.1.2 Association en parallèle

En parallèle l’inverse de la résistance équivalente est égale à la somme des inverses des résistances placées en parallèle :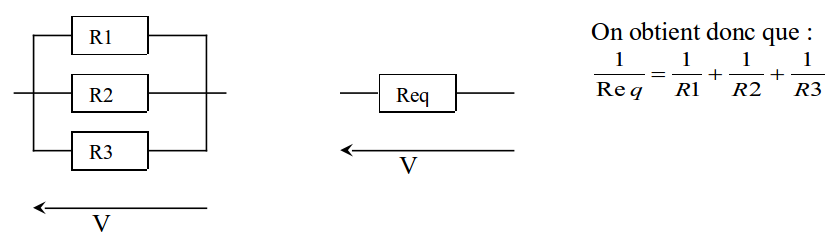

Généralisation :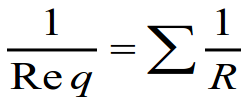

Cas particulier de 2 résistances en parallèle :
 

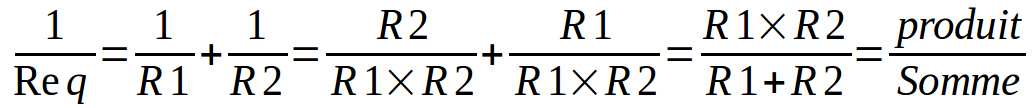
On mémorise souvent cette forme : la résistance équivalente à 2 résistances en parallèle est le produit des 2 résistances sur leur somme.

Cela ne fonctionne qu’avec 2 résistances !

 
1.2. La loi d'ohm


Cette loi exprime le lien de proportion entre la tension aux bornes d’une résistance R et le courant qui la traverse:

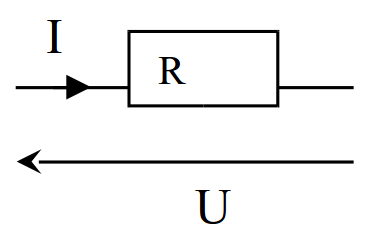Loi d’Ohm : U = R I

1.3. Les lois de Kirchhoff

1.3.1    La loi des nœuds

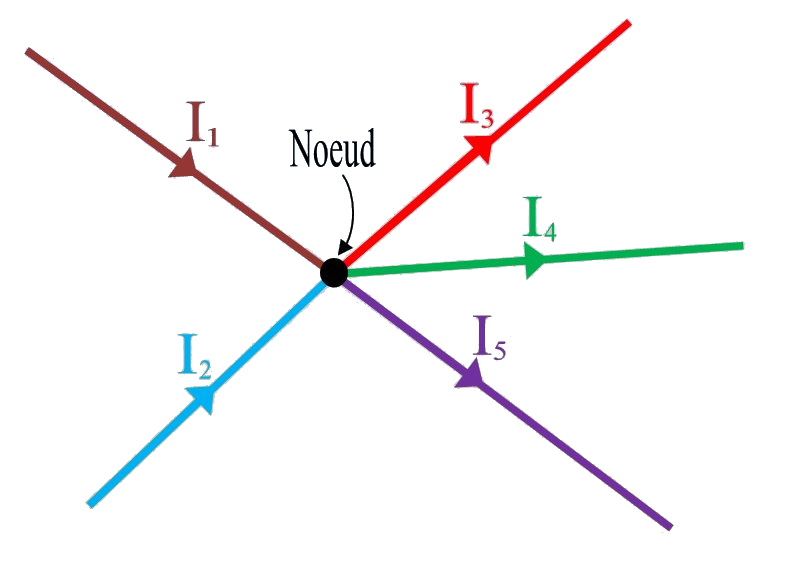
Loi des nœuds (ou loi de Kirchhoff pour les courants) : La somme algébrique des courants (on tient compte de leur signe) qui convergent en un même nœud est nulle :

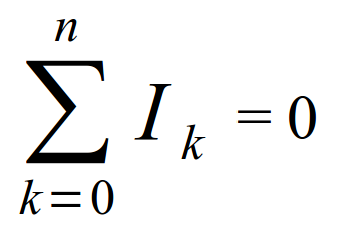	Ici :  I1 + I2 – I3 – I4– I5  = 0

on peut aussi formuler la loi des nœuds de la façon suivante : la somme des courants qui « rentrent » est égale à la somme des courants qui « sortent ». On obtient alors I1 + I2 = I3 + I4 + I5

1.3.2    La loi des mailles

Une maille est un circuit électrique fermé, pouvant contenir des générateurs et/ou des récepteurs.

Loi des mailles : dans une maille, la somme algébrique (on tient compte de leur signe) des tensions est nulle : ΣU=0
 

Règles pour résoudre les exercices:

On flèche les courants
On flèche les tensions
On choisir un sens de parcours des mailles
On écrit les équations de mailles

Exemple :

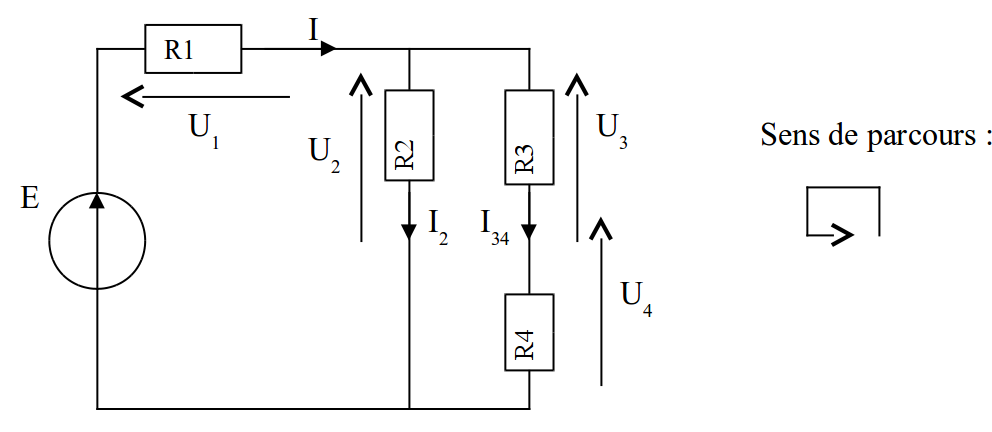
On peut écrire 3 mailles :  

• U2 + U1 – E = 0
• U4 + U3 + U1 – E = 0
• U4 + U3 – U2 = 0

	Remarque 1 : On peut aussi écrire les mailles en faisant intervenir les résistances et les courants. Ainsi la première maille U2 + U1 – E =0 peut aussi s’écrire: (R2×I2) + (R1×I) – E =0
	Remarque 2 : pour résoudre un exercice, on écrira toujours toutes les équations de nœuds. Par contre on ne peut écrire, si l’on veut, que les équations de mailles utiles.