Logique combinatoire
Remarque: l'exercice est disponible en version "interactive" sur l'intranet du lycée (Moodle) dans la rubrique (cours) "1STI - Révisions I2D (Enseignement technique et professionnel)"
Durée prévue : 1h15
Objectifs : Révisions de la logique combinatoire
Prérequis : Les bases de la numération (binaire et décimal) et de la logique
Modalités : Exercices sur le site internet : https://sti2d.ecolelamache.org/
Documents ressources : Cours et TP sur la logique combinatoire
Exercice 1 : circuits logiques de base
Porte OU :
a) Donnez les symboles (européen et américain) de la porte OU :
b) Compléter la table de vérité :
|
A |
B |
S |
|
0 |
0 |
|
|
0 |
1 |
|
|
1 |
0 |
|
|
1 |
1 |
Porte Non-OU (NOR):
c) Donnez les symboles (européen et américain) de la porte NOR:
d) Compléter la table de vérité :
|
A |
B |
S |
|
0 |
0 |
|
|
0 |
1 |
|
|
1 |
0 |
|
|
1 |
1 |
Porte OU Exclusif (XOR):
e) Donnez les symboles (européen et américain) du OU exclusif :
f) Compléter la table de vérité :
|
A |
B |
S |
|
0 |
0 |
|
|
0 |
1 |
|
|
1 |
0 |
|
|
1 |
1 |
Porte ET :
g) Donnez les symboles (européen et américain) de la porte ET :
h) Compléter la table de vérité :
|
A |
B |
|
|
0 |
0 |
|
|
0 |
1 |
|
|
1 |
0 |
|
|
1 |
1 |
Exercice 2 : petits circuits logiques
Dessinez le schéma logique (logigrammes suivant la norme européenne) des équations suivantes :
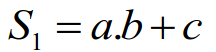
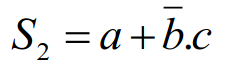
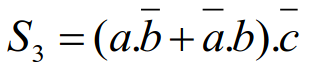
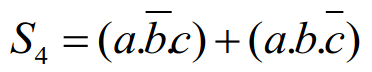
Exercice 3 : des circuits logiques inconnus à analyser.
Circuit N°1 : soit le logigramme suivant :
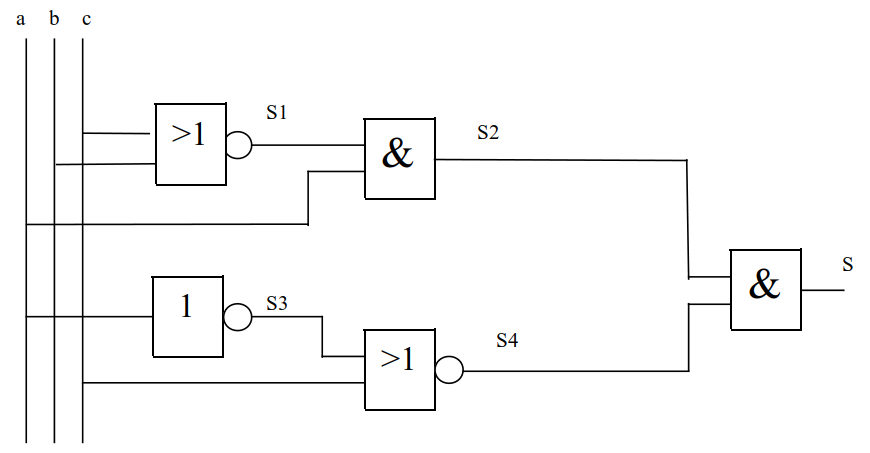
1. Donner l’équation de chaque sortie de portes logiques (S1, S2, S3, S4 et S)
2. En déduire les tables de vérité de chaque sortie.
|
a |
b |
c |
S1 |
S2 |
S3 |
S4 |
S |
|
0 |
0 |
0 |
|||||
|
0 |
0 |
1 |
|||||
|
0 |
1 |
0 |
|||||
Circuit N°2 : soit le logigramme suivant :

1. Complétez la table de vérité suivante (des variables intermédiaires ont été ajoutée comme c0, e0, … afin de faciliter la résolution)
|
B2 |
B1 |
B0 |
A2 |
A1 |
A0 |
c0 |
d0 |
e0 |
f0 |
c1 |
d1 |
e1 |
f1 |
c2 |
d2 |
e2 |
S2 |
S1 |
S0 |
Rout |
|
|
Cas 1 |
0 |
0 |
1 |
0 |
0 |
1 |
|||||||||||||||
|
Cas 2 |
0 |
1 |
0 |
0 |
1 |
1 |
|||||||||||||||
|
Cas 3 |
1 |
1 |
0 |
0 |
0 |
1 |
|||||||||||||||
|
Cas 4 |
1 |
1 |
1 |
0 |
0 |
1 |
Essayons de comprendre ce que réalise ce circuit logique.
B0, B1 et B2 représentent un chiffre codé sur 3 bits (de même que A0, A1 et A2 et aussi S0, S1 et S2).
2. Complétez le tableau suivant avec les valeurs décimales de ces 3 chiffres
|
Chiffre B |
Chiffre A |
Chiffre S |
|
|
Cas 1 |
|||
|
Cas 2 |
|||
|
Cas 3 |
|||
|
Cas 4 |
3. Déduisez des 3 premiers cas du tableau précédent la fonction réalisée par ce circuit logique
4. En vous aidant du cas 4, expliquez à quoi sert la sortie Rout ?
Exercice 4 : exemple réel
Description du fonctionnement:
Un appareil comporte trois cuves contenant de l’eau, du cassis et de la menthe. Trois boutons (e, m, c) commandent les électrovannes (E, M, C). Les électrovannes permettent d’obtenir de l’eau pure, de la menthe à l’eau ou du cassis à l’eau. Une pièce (p) est nécessaire pour obtenir une boisson à la menthe ou au cassis. L’eau pure est gratuite.
Le déclenchement d’un bouton quelconque (e, m, c) ou l’introduction de la pièce déclenche une temporisation (la temporisation n’est pas traitée). Si celle-ci arrive à son terme avant qu’un choix cohérent ait été fait, cette pièce est rendue (fonction P de restitution). La pièce est également rendue en cas de fausse manœuvre.
Ainsi pour obtenir de la menthe à l’eau (E et M) il faut mettre une pièce (p) et appuyer sur m (ou sur e et m), ...
1) Remplir la table de vérité suivante (4 entrées, 4 sorties)
|
entrée |
sorties |
||||||
|
e |
m |
c |
p |
E |
M |
C |
P |
|
0 |
0 |
0 |
0 |
||||
|
0 |
0 |
0 |
1 |
||||
|
0 |
0 |
1 |
0 |
||||
|
0 |
0 |
1 |
1 |
||||
|
0 |
1 |
0 |
0 |
||||
2) Tirer de la table de vérité les équations des quatre sorties
E=
M=
C=
P=
En Bonus
Exercice 5 : circuit logique inconnu
Soit le schéma suivant :
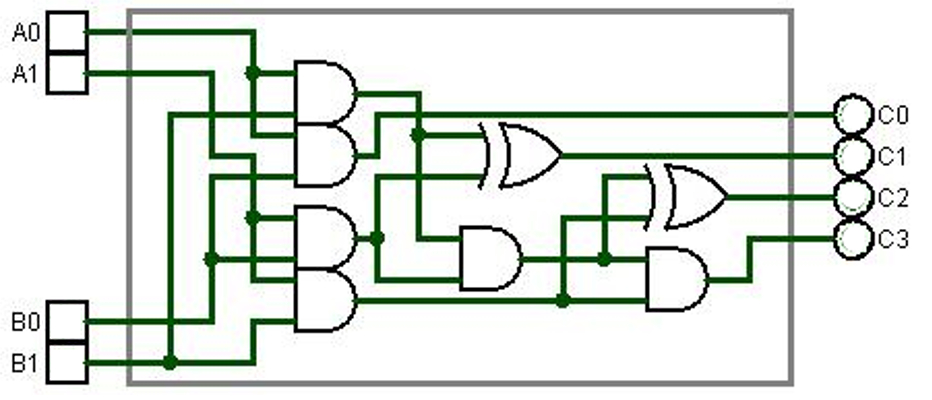
Appliquez une démarche similaire à l'exercice 3 pour trouver (et démontrer) le rôle de ce circuit logique.