Exercice N°4 : descente de charge

Nous allons nous occuper de la structure d'un abris carré de 5*5m (permettant de garer voiture, deux roues , ...) et possédant un toit végétalisé1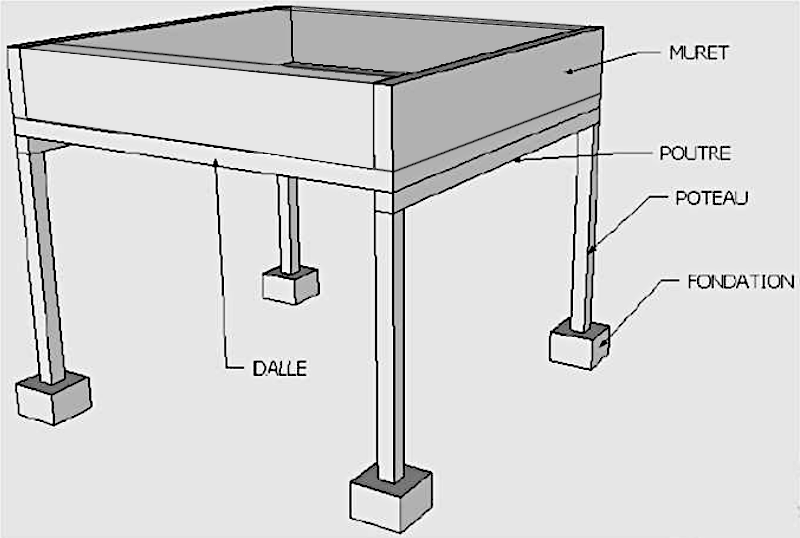

 
La structure est composée de plusieurs constituants en béton armé dont il faut évaluer la masse pour évaluer les effets de la pesanteur.
La masse volumique du béton armé est de 2500 kg/m³. La masse volumique de la terre (remplissage de la partie délimitée par le muret) est de 1250 kg/m³

 

Rappel: g=9.81 m.s^-2

Voici les dimensions des différents éléments:

 

Dans cet exercice, on ne va s'occuper que des charges permanentes. Celles-ci sont due à:

1. à la charge variable due à l’usage prévu?
2. au poids propre de la structure?
3. à la charge liée aux aléas climatiques?

 

Calculons la masse de notre abris

 
Calculer le volume de terre du toit: Vt =      m³

Calculer la masse de terre: Mt =       kg

Calculer le poids de la terre:            N

 

Compléter maintenant le tableau ci-dessous:

élément	volume (m3)	masse (kg)	Masse (N)
dalle
1 poutre
1 poteau
1 semelle
muret

 

Qui supporte qui?

L’analyse de la structure nécessite d’évaluer comment les charges sont transmises d’un composant à un autre. Il faut donc identifier « QUI SUPPORTE QUI ».

Voici la structure de notre abris (à compléter en dessous):

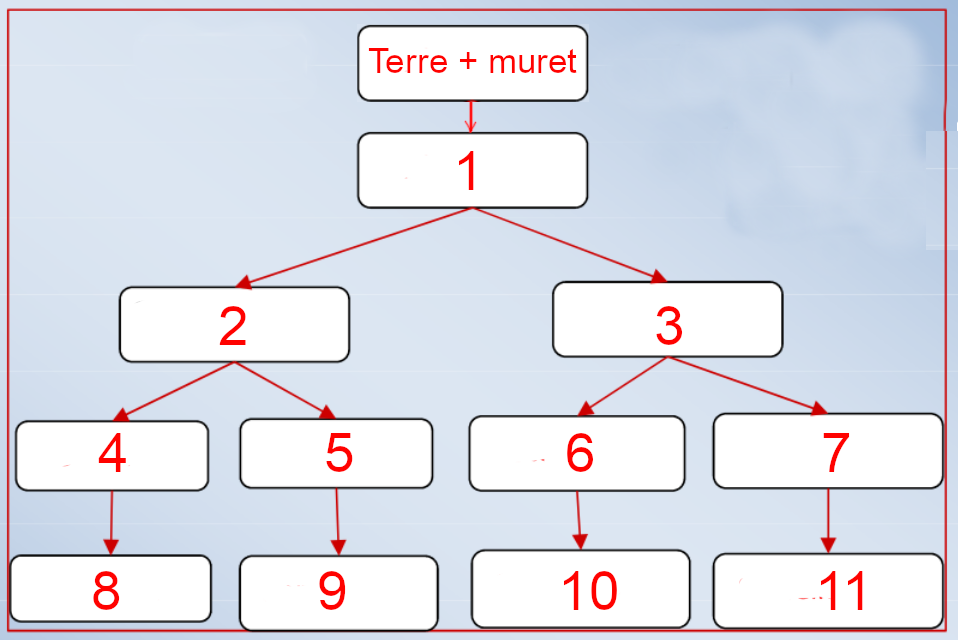
La terre et le muret (élément 0) pèsent sur l'élément 1.

Dire, pour chaque élément (1, 2 ...) ce qu'il est dans la structure ci-dessus:

1. une semelle?
2. la dalle?
3. un poteau?
4. une poutre?
   

 
Bilan: notre structure est-elle correcte au niveau des fondation?

A partir de ce que l'on a fait , calculer la charge totale qui s'exerce à la base de chaque fondation (chaque semelle): F =      N

 
On va maintenant calculer la contrainte de compression σ (sigma) en MPa. On utilise la formule suivante : σ=F/S . F est la force appliquée sur la surface S. Si on calcule S en mm², on obtient une contrainte en MPa (mega Pascal)

Calculer la surface d'une de nos fondation (une semelle) :        mm²

Calculer la contrainte de compression exercée sur le sol par une de nos fondation (une semelle): σ =      MPa

 

On applique un coeffiscient de sécurité de 1,5.

Calculer la nouvelle contrainte de compression exercée sur le sol par une de nos fondation (semelle): σ =   MPa
 

Si la contrainte max du sol est de 1 MPa , les fondations sont elles suffisantes ?