Exercice N°1: petits exercices
Remarque: les exercices sont disponibles en version "interactive" sur l'intranet du lycée (Moodle) dans la rubrique (cours) " 1STI - Révisions I2D (Enseignement technique et professionnel)"
Exercice N°1: Calcul du moment d’une force :
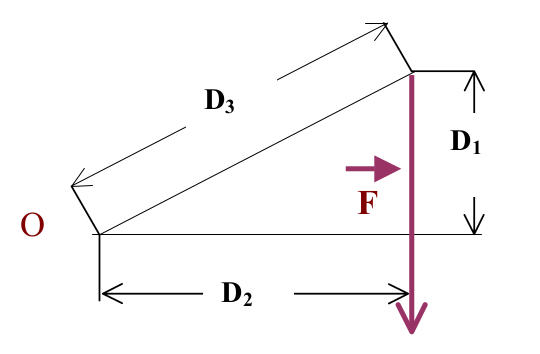
Application numérique : D1 = 3 m ; D2 = 4 m ; D3 = 5 m et F= 200 N
Quel est le moment M de la force F par rapport au point O ?
Exercice N°2 : Modifications des caractéristiques de la force (point d’application et intensité):
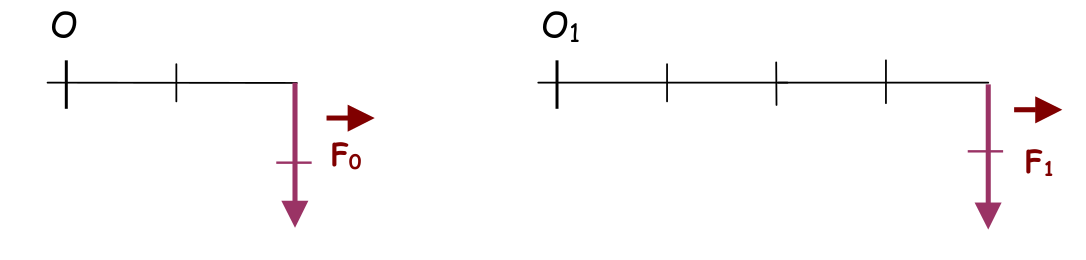
Remarque: l’intensité de la force F1 est égale à l’intensité de la force F0
Q1: Le moment de la force F1 par rapport à O1 , est égal à X fois le moment de la force F0 par rapport à O. Trouvez ce coefficient X.
Modifications des caractéristiques de la force (point d’application et intensité):
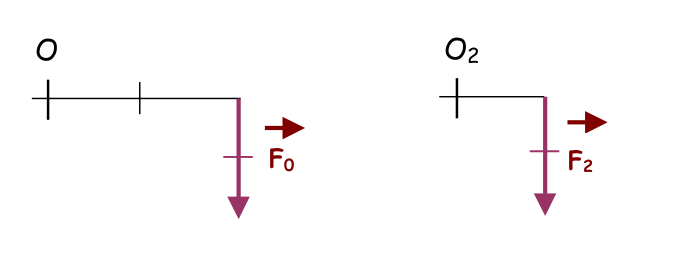
Remarque: l’intensité de la force F2 est égale à l’intensité de la force F0
Q2: Le moment de la force F2 par rapport à O2 , est égal à X fois le moment de la force F0 par rapport à O. Trouvez ce coefficient X.
Modifications des caractéristiques de la force (point d’application et intensité):
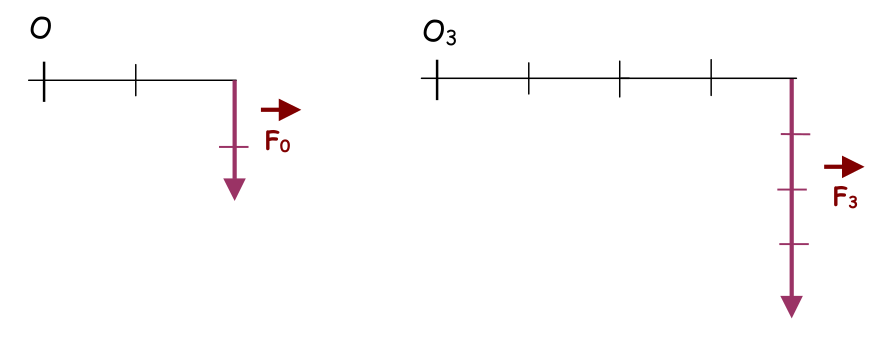
Remarque: l’intensité de la force F3 est égale à 2 fois l’intensité de la force F0
Q3: Le moment de la force F3 par rapport à O3 , est égal à X fois le moment de la force F0 par rapport à O. Trouvez ce coefficient X.
Modifications des caractéristiques de la force (point d’application et intensité):
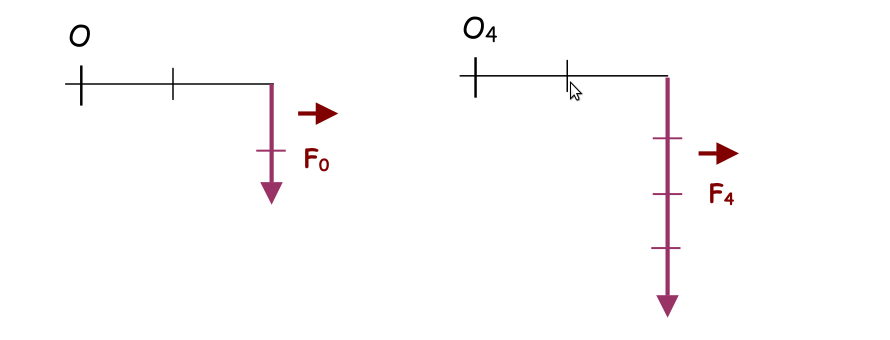
Remarque: l’intensité de la force F4 est égale à 2 fois l’intensité de la force F0
Q4: Le moment de la force F4 par rapport à O4 , est égal à X fois le moment de la force F0 par rapport à O. Trouvez ce coefficient X.
Modifications des caractéristiques de la force (point d’application et intensité):
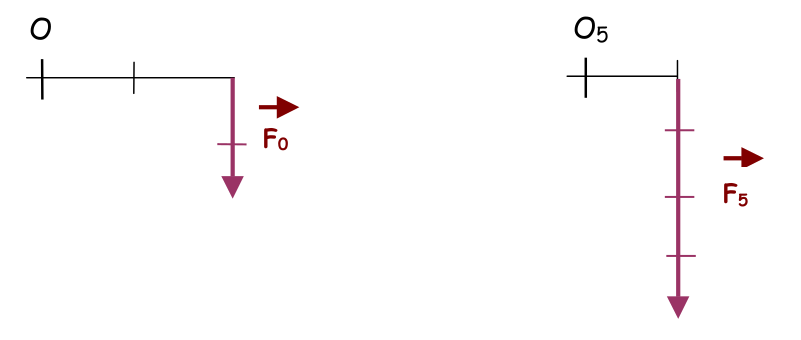
Remarque: l’intensité de la force F5 est égale à 2 fois l’intensité de la force F0
Q5: Le moment de la force F5 par rapport à O5 , est égal à X fois le moment de la force F0 par rapport à O. Trouvez ce coefficient X.
Exercice N°3 : Cas d’un solide suspendu :
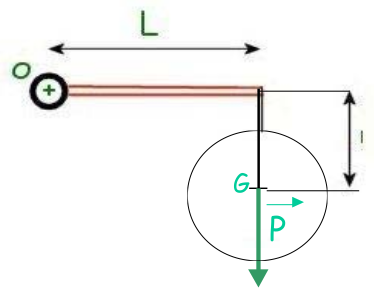
L = 3m ; l = 1,5 m ; La sphère a une masse de 20 kg. Prendre 9,81 m/s2 pour valeur de l’accélération de la pesanteur.
Quel est le moment M exercé par le poids de cette sphère, par rapport au point O (avec un chiffre aprés la virgule) ?
Exercice N°4 : cas de plusieurs forces
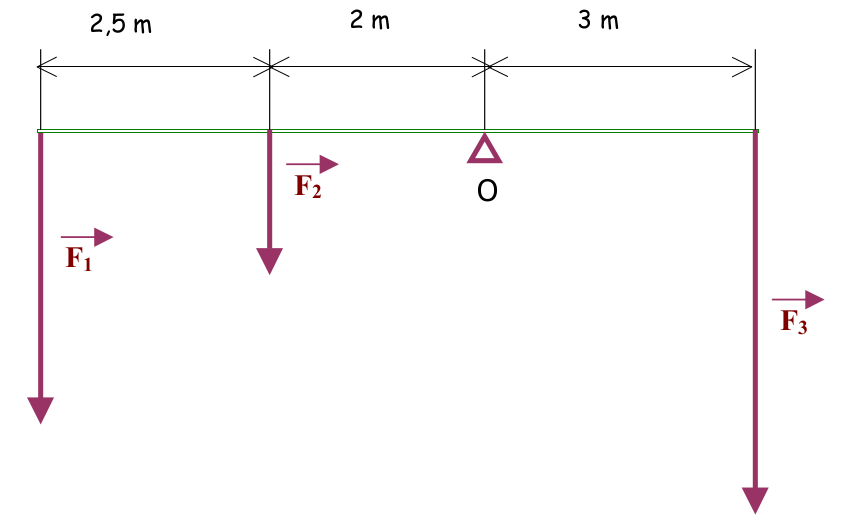
F1 = 200N ; F2 = 100N et F3 = 250N
Q1 : Quelle est la valeur absolue du moment M résultant de l’ensemble de ces 3 forces ?
Q2 : Dans quel sens la barre va-t-elle tourner ?
Exercice N°5 : recherche de l'équilibre
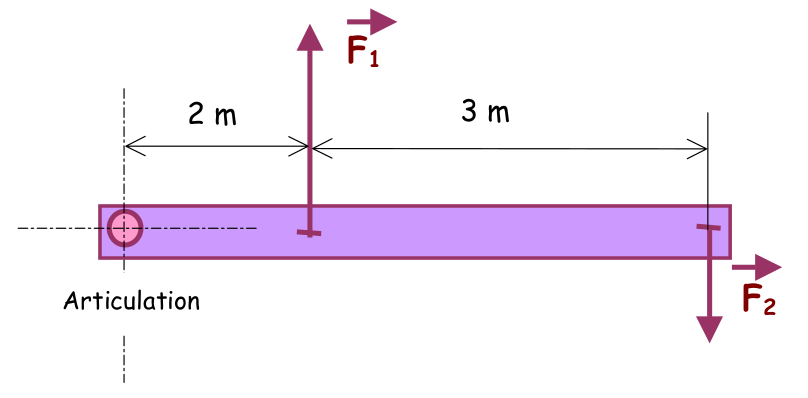
F 1 = 300 N
Quelle doit être l’intensité de la force F 2 pour que ce système reste en équilibre ?
Recherche de l'équilibre:
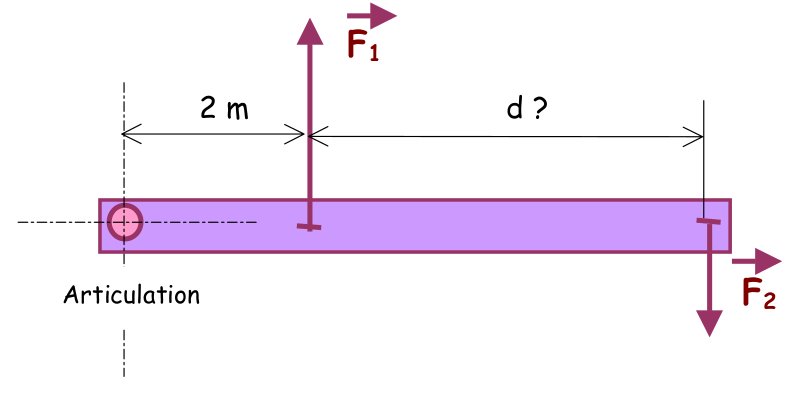
F 1 = 300 N
Si l’intensité de F2 est 100 N, à quelle distance d de F1 devrait se situer le point d’application de la force F2 pour maintenir l’équilibre ?
Exercice N°6 : cas où la direction de la force n’est pas perpendiculaire au bras de levier :
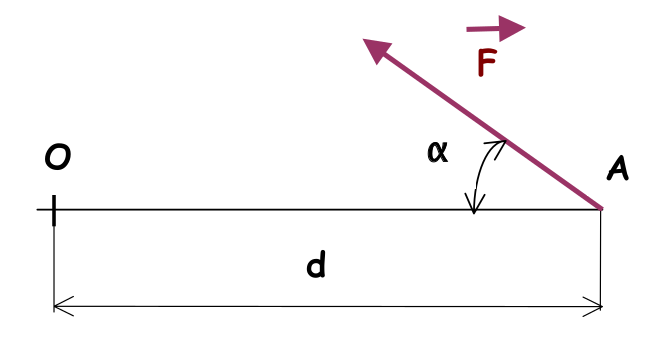
Donnez la formule du moment de la force F par rapport au point O:
Exercice N°7 : stabilité et basculement :
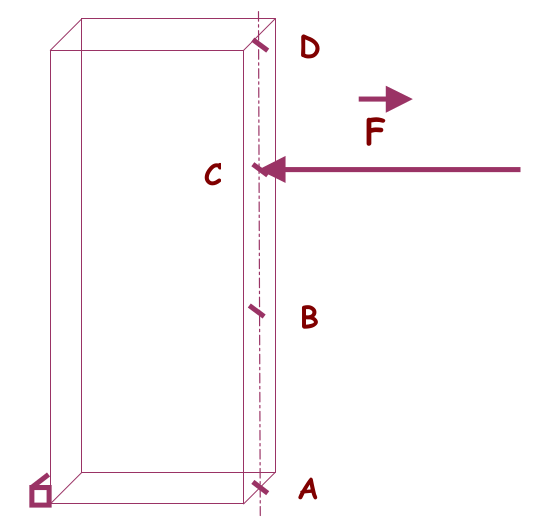
AB = 2 m, AC = 3 m, AD = 4 m
Q1: si la force F a une intensité de 1000 N, le bloc est à la limite de l’équilibre, que se passe–t-il si on applique la force F au point B ?
Q2 : si la force F a une intensité de 1000 N, le bloc est à la limite de l’équilibre. Que se passe–t-il si on applique la force F au point D ?
Q3 : que se passe–t-il si la force F, appliquée en C, a une intensité de 1100 N ?
Q4 : que se passe-t-il si on applique une force F de 800 N au point D ?
Q5 : l’intensité maximale de la force que l’on peut appliquer en C pour que le bloc ne bascule pas est de 1000 N. Quelle est l'intensité minimale de la force F' appliquée en D pour que le bloc bascule ?
Q6 : que se passe–t-il si on applique une force F de 800 N au point B ?
Q7 : sachant que 1 000 N est l’intensité maximale de la force qu’on peut appliquer en C pour que le bloc ne bascule pas, quelle est l'intensité minimale d'une force F' appliquée en B pour que le bloc bascule ?
Exercice N°8 : le coupe boulon :
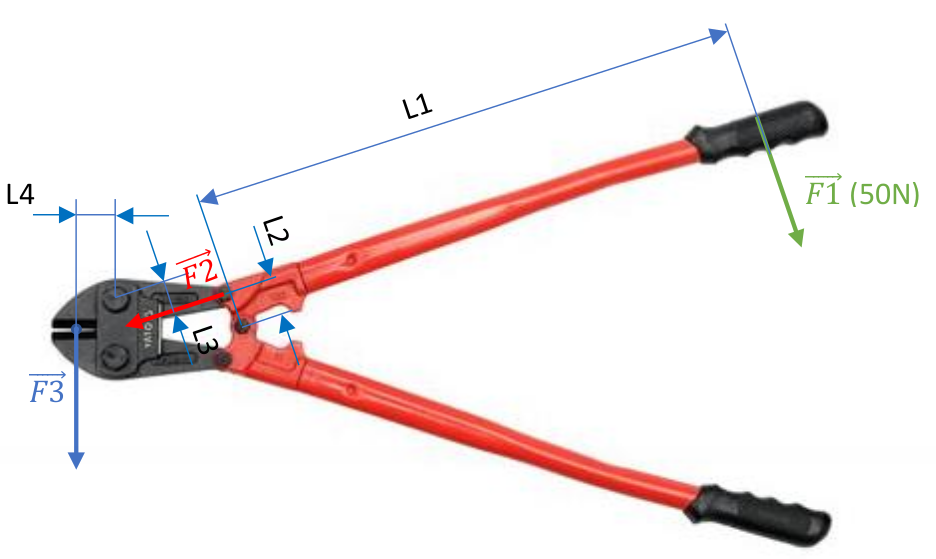
L1 = 680 mm, L2 = 44 mm, L3 = 36 mm, L4 = 40 mm.
Si l’effort F1 , appliqué par l’utilisateur, a une intensité de 50 N, quelle est l’intensité de la force F3, appliquée par la lame sur le câble à couper ?
Étapes utiles à la résolution:
- Calculez le moment de la force F1 exercée par l’utilisateur, par rapport à la 1ère articulation
- En déduire l'intensité de la force intermédiaire, notée F2. Calculez le moment de la force F2 par rapport à la deuxième articulation (celle du mors)
- En déduire l'intensité de la force F3
Exercice N°9: forces et vecteurs (géométrie)
Remarque: dans les exercices ci-dessous, toutes les forces si situent dans le même plan (x,y)
Partie 1: soit la force F de norme 40N. α=69°
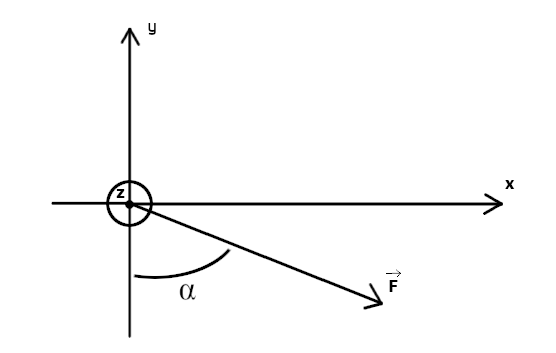
Calculer les coordonnées du vecteur F:
- Fx = N
- Fy = N
- Fz = N
Partie 2: soit la force F:
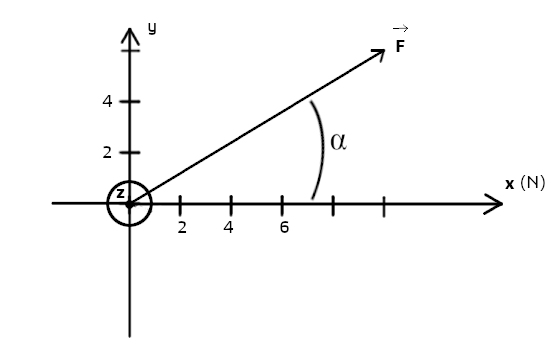
Relever les coordonnées de la force F:
- Fx = N
- Fy = N
- Fz = N
Calculer la norme du vecteur F: F = N
Calculer l'angle α : α= °
Partie 3: soit les trois forces suivantes:
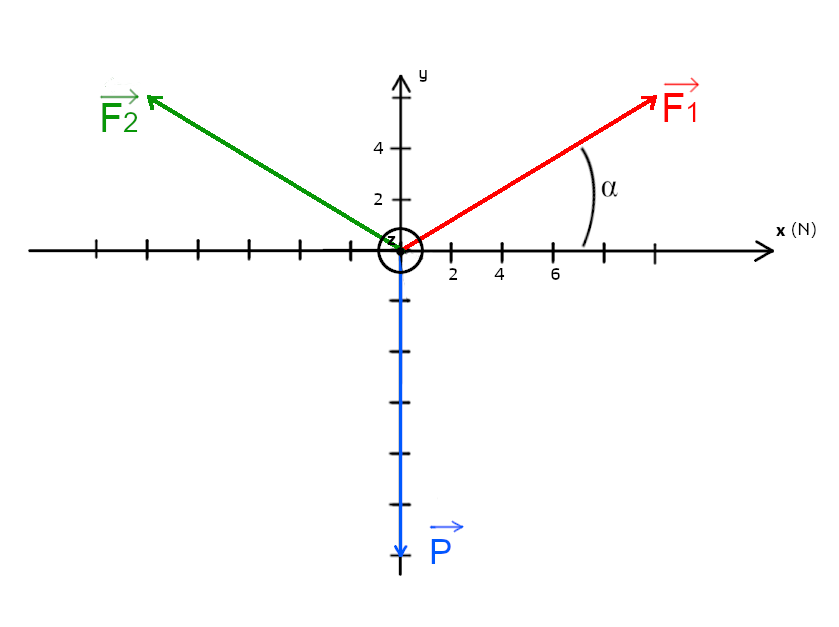
Donner les coordonnées des 3 forces:
Px : N F1x = N F2x= N
Py : N F1y = N F2y= N
Pz : N F1z = N F2z= N
Calculer les coordonnées de la force résultante:
Rx = N
Ry = N
Rz = N
Calculer la norme du vecteur R: R = N
Conclusion:
- la situation du système est inconnue?
- le système est en mouvement?
- le système est à l'équilibre?